定义3-1 n个随机变量X1,X2,…,Xn构成的整体X=(X1,X2,…,Xn)称为一个n维随机变量或n维随机向量,Xi称为X的第i(i=1,2,…,n)个分量.
定义3-2 设(x,Y)为一个二维随机变量,记
F(x,y)=P{X≤x,Y≤y},-∞
称二元函数F(x,y)为X与y的联合分布函数或称为(X,Y)的分布函数.
(X,Y)的两个分量X与y各自的分布函数分别称为二维随机变量(X,Y)关于X与关于y的边缘分布函数,记为FX(x)与FY(y).
边缘分布函数可由联合分布函数来确定,事实上,一元函数
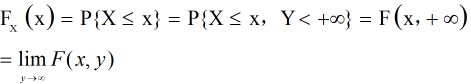
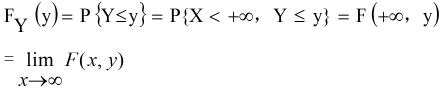
几何上,若把(X,Y)看成平面上随机点的坐标,则分布函数F(x,y)在(x,y)处的函数值就是随机点(X,Y)落在以(x,y)为顶点、位于该点左下方的无穷矩形D内的概率.
分布函数F(x,y)具有下列性质:
(1)F(x,y)是变量x(或y)的不减函数.
(2)0≤F(x,y)≤l,
对任意固定的y,F(-∞,y)=0
对任意固定的x,F(x,-∞)=0;
F(-∞, -∞)=0,F(+∞,+∞)=1.
(3)F(x,y)关于x和关于y均右连续,即
F(x,y)=F(x+0,y);F(x,y)=F(x,y+0).
(4)对任意固定的x1
F(x2 ,y2)-F(x2,yl)-F(xl,y1)+F(x1+yl)≥0.
(责任编辑:liushengbao)
近期直播
免费章节课
课程推荐
自考
[Vip签约通关班]
准题库自主练习校方服务
自考
[尊享考霸签约班]
准题库自主练习校方服务
自考
[Vip签约通关连续班]
准题库自主练习校方服务
